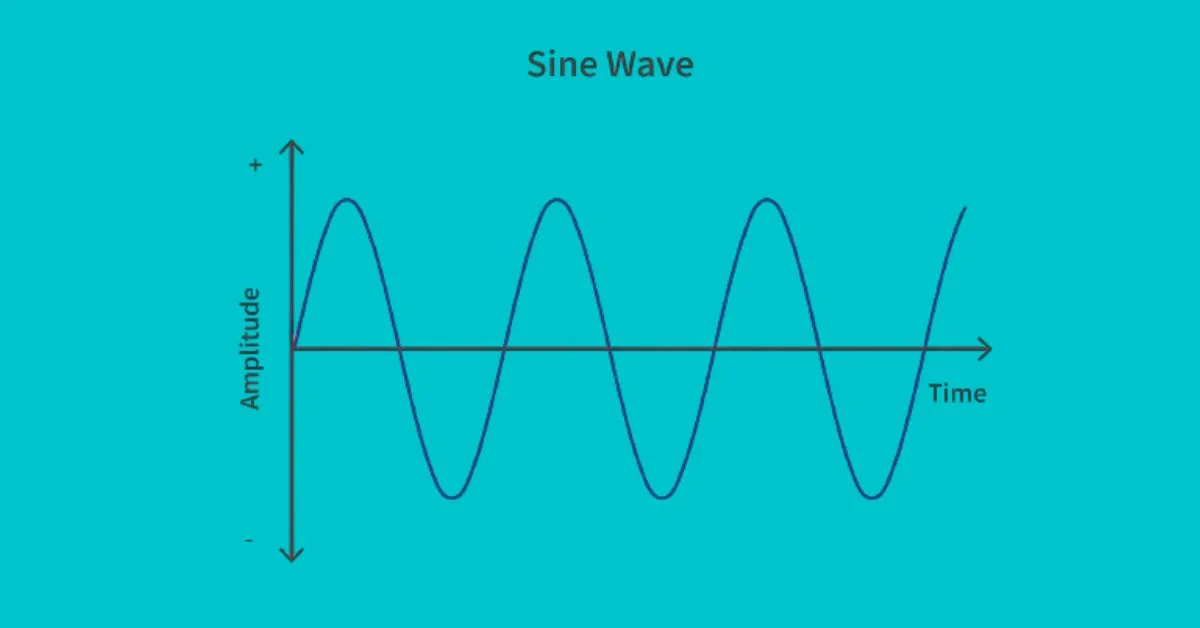
To start, sine waves are basic mathematical functions that are important in many different areas, including signal processing, engineering, and physics. Various natural phenomena, such as sound waves, light waves, and the swing of a pendulum, exhibit periodic oscillations, which these symbols depict. The equation that describes a sine wave is y(t)=Asin(ϋt+ϕ)y(t) = A \sin(\omega t + \phi)y(t)=Asin(ϋt+ϕ), where AAA is the amplitude, ω\omegaϋ is the angular frequency, ttt is the time variable, and ϕ\phiϕ is the phase shift.
Exploring the Components of a Sine Wave
It is necessary to comprehend the parts of sine wave modelling before delving further into it. How “tall” or “short” the wave seems is simply described by the amplitude AAA, which defines the peak value of the wave. Where the wave begins in relation to the origin is determined by the phase shift ϕ\phiϕ, and the angular frequency ω\omegaϋ specifies the rate of oscillation. You may simulate several kinds of sine waves with varying properties by changing these parameters.
The Significance of Amplitude in Sine Waves
A sine wave’s amplitude determines how it looks and how it behaves generally. A sound’s volume or a light’s brightness might be two real-world examples of amplitude’s usefulness. A sine wave’s height grows in relation to its amplitude, suggesting a stronger oscillation. To the contrary, a flatter wave, signifying less intensity, is the outcome of decreasing the amplitude.
Analyzing Frequency and Period of Sine Waves
Knowing the duration and frequency is also crucial for sine wave modelling. In Hertz (Hz), the frequency fff is defined as the number of oscillations per unit of time. The equation f=ω2πf = \frac{\omega}{2\pi}f=2πωshows a clear relationship to the angular frequency. In contrast, the time it takes for one full wave cycle, denoted as TTT, is inversely proportional to frequency, with T=1fT = \frac{1}{f}T=f1. You may make the wave look “fast” or “slow” by adjusting the frequency.
The Role of Phase Shift in Sine Waves
In sine wave modelling, another crucial component is the phase shift ϕ\phiϕ. Here we can see the wave’s horizontal displacement. When the phase shift is positive, the wave is shifted to the left, and when it is negative, it is shifted to the right. Applications requiring wave synchronization, like communication systems, might benefit greatly from this. Signal alignment is crucial for effective transmission.
Constructing a Sine Wave Model: Step-by-Step Guide
It is helpful to know what you want out of the sine wave model before you build it. Get the amplitude, frequency, and phase shift right by considering your application’s needs. Then, to create the wave, use the sine function as follows: y(t)=Asin(ϋt+ϕ)y(t) = A \sin(\omega t + \phi)y(t)=Asin(ϋt+ϰ). For this, you may use Excel, Python, or MATLAB, among other software tools.
Practical Applications of Sine Wave Modeling
Theoretically, sine wave modelling is sound, but in practice, it finds many uses. For example, in the realm of electronics, alternating current (AC) signals are characterized by sine waves. When it comes to signal processing and sound synthesis, they are cornerstones of audio engineering. Also, in physics, oscillating motions like pendulums or mass-spring systems are represented by sine waves.
Advanced Sine Wave Modeling Techniques
Fourier analysis and other methods can be used to expand sine wave modelling for more complicated applications. The process begins with breaking down the original waveform into its component sine waves, which may then be varied in terms of both frequency and amplitude. This allows you to study and reproduce signals that would be hard to characterize with just a sine wave.
Common Challenges in Sine Wave Modeling
Sine wave modelling has many uses, but it also has its limitations. In systems where synchronization is crucial, precisely recording the phase shift is one of the most prevalent challenges. Furthermore, the model could be inaccurate due to numerical mistakes that occur during digital sine wave generation. Being alert to these possible problems and taking action to fix them is of the utmost importance.
Best Practices for Accurate Sine Wave Modeling
Adhering to established practices is crucial to guaranteeing the correctness of your sine wave models. Make sure the amplitude, frequency, and phase shift are all correct before you generate the wave. Also, to keep numerical mistakes to a minimum, make use of precise instruments and software. Lastly, think about applying Fourier analysis to simplify the waveform when modelling complicated systems.
Conclusion
To sum up, sine wave modelling is a vital resource for many fields of engineering and science. Accurate models of real-world occurrences may be created by comprehending and adjusting characteristics including amplitude, frequency, and phase shift. Sine wave modelling is a skill that may be applied in many different contexts, from fundamental signal processing to expert Fourier analysis.
FAQs
1. What is the primary use of sine wave modeling?
Many disciplines, including engineering, signal processing, and physics, rely on sine wave modelling to depict periodic oscillations.
2. How does amplitude affect a sine wave?
The sine wave’s “height” and the strength of its oscillations are affected by the amplitude, which in turn influences the peak value.
3. What is the relationship between frequency and period?
Period is the amount of time it takes for a complete cycle, while frequency is the number of oscillations per unit of time. Their relationship is inverse.
4. Why is phase shift important in sine wave modeling?
An essential component for signal synchronization in systems like communication networks, phase shift defines the horizontal displacement of the sine wave.
5. What tools can be used for sine wave modeling?
Because of their robust mathematical functions and graphical capabilities, tools such as MATLAB, Python, and Excel are frequently utilized for sine wave modelling.